ヒスあれこれ ― SOMETHING ABOUT HISS

【】内は草稿部分、全体を継続資源としてすこしずつてなおししていきます
—

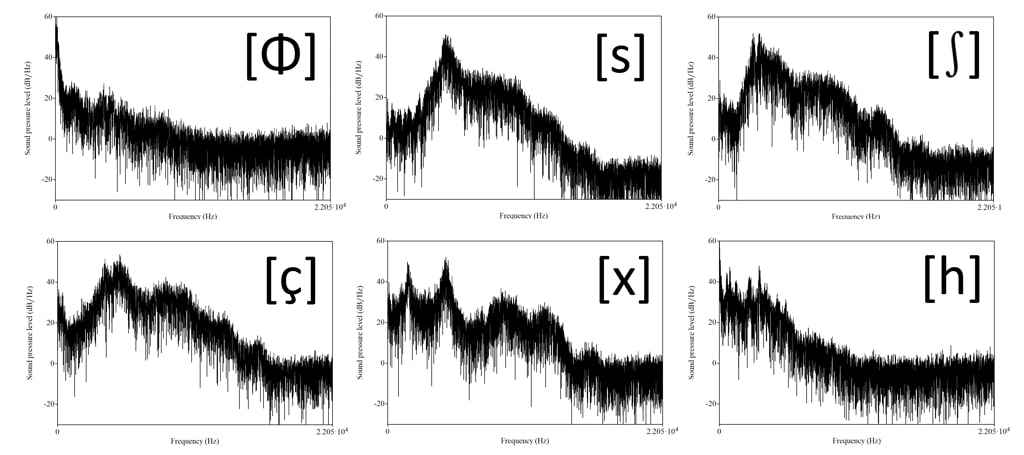
キャットフォードの音声学教科書*1に「吐き出す息の音（特定されない呼気の音）[h]」としてヒス音（乱流音つまりランダム渦の音、周期性をもたないノイズ音の1例、EG. 日本語で書くなら声帯を響かせない音としてのフー・スー・ヒー・グゥ・ハー音など無声の加声変調/PHONATIONにて継続的に生産される声道音）があげられている また閉鎖調音（EG.[p][t][k]）における音声生産開始前後における特定のヒス音の挙動について、同書の“2.2摩擦音と閉鎖音の調音”［原著ではFRICATIVE AND STOP ARTICULATION/摩擦調音&閉鎖調音である またそれら調音による生産音はそれぞれ音響学的に乱流音・ポップ音とも称される］・“2.3肺の圧搾と吸引による始動”・“3.9気音”あたりの項に図をもちいたくわしい説明がある

ここでは、科学的明瞭さをすこしでも理解加勢するために、維持区間/DULATIONをもった定常音としてのヒス音（始動/INITIATION・加声変調（内・外の収音過程を含む）における過渡音/TRANSITIONや、音響学でいうポップ音/POP・ハム音/HUM・ゴロゴロ音/BUZZなど非ヒス音・システマティック音には言及しない）の物理学とその自然現象の科学記述法（とくに周波数軸関数の虚数記述表現が内包的に意味する時間変動概念）についてなるべく数量学にたよらずに説明をこころみる（空気の流体力学とフーリエ変換をもうすこし知りたい人などにむける）

1、ホワイトノイズ
ホワイトノイズは「RBW[Hz]（解像帯域幅）内の信号パワ[W]（≙エネルギー流の量[J/s]）が関心ある広帯域全域で同一とみなせるエネルギー流の総合的な束/FLUX[W]」と定義される（=パワ=強度/intensity[W]、またはパワ密度[W/m^2]をもちいて面積通過部分の「強度」を分布として定義する場合もある） これは周波数的に平坦なスペクトラム特性とよばれる
（現象例）
滝川の岩ばしるせせらぎ音波（信号パワが音圧パワである1例）をある時間区間/SEGMENTでとりだしたのち、さらに音の高さ（周波数帯）で分けて個別にとりだしたとき、どの周波数帯であってもそれを受ける完全理想吸音材はおなじだけの音圧パワ累積を区間内に吸収する（たとえばせせらぎ音波の100-105[Hz]をまとめて弁別した束と200-205[Hz]のそれとでは、区間内の束の累積印加結果として、音波を受ける完全理想吸音材をおなじだけ温度上昇させる）

2、声道内外で発生するヒス音
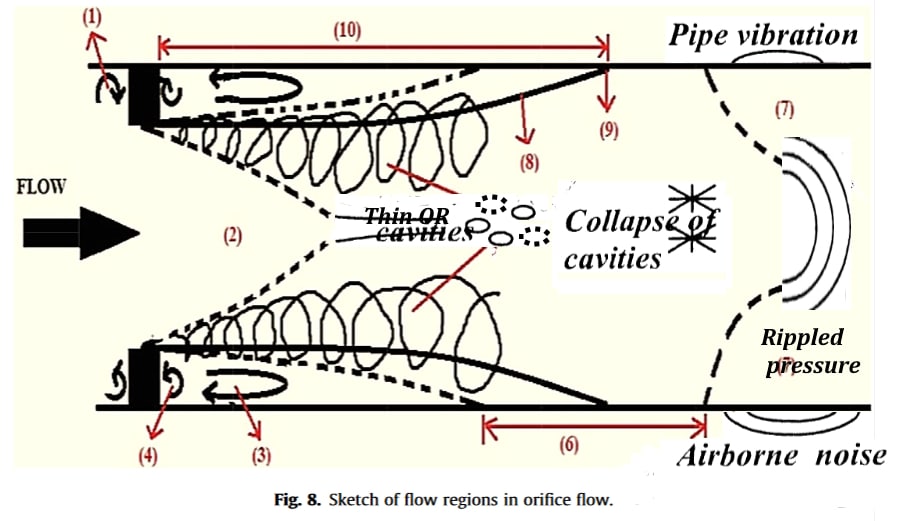
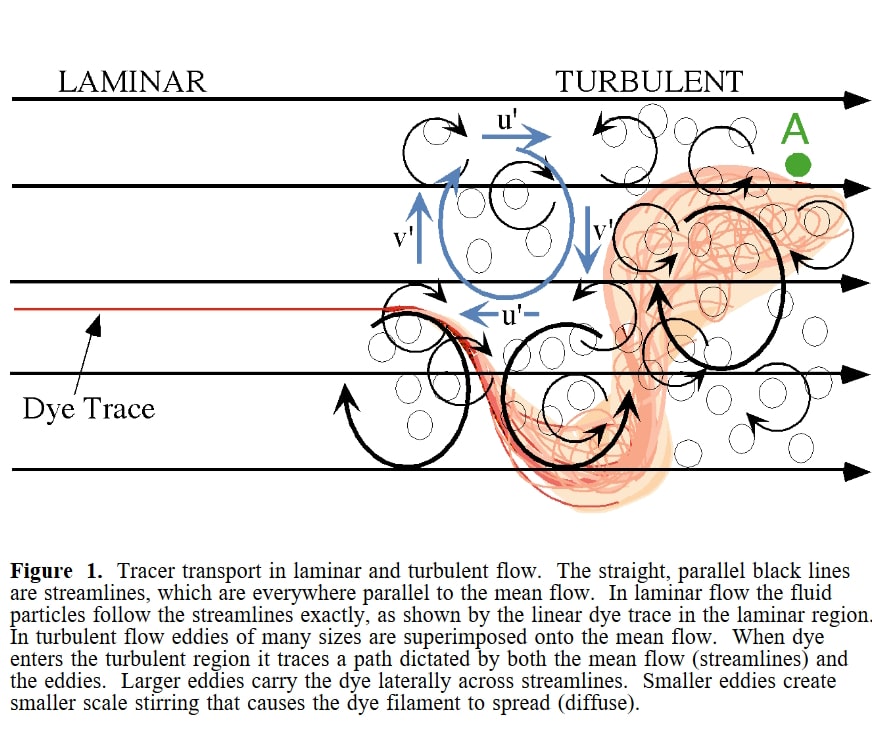
ヒス音/HISSING SOUNDは乱流/TURBULENT FLOW（層流/LAMINAR～の対義語）からの音波（=音響波∈機械振動）発生現象をあらわし、押されて障害物近くから広空間にでてきた粘性流体が元からそこにあった流体空間静止状態からのゆり戻し力を反作用としてうけることにより渦/EDDIESの種がまず発生し、それが次々と分割されてさらなる微細擾乱構造へと運動エネルギーをリレーしていくことで結果として乱流要素がランダムに分布するものである（乱流成長機序は不明とされる）
説明のため、大気圧をうけた温度をもつ空気分子分布状態を、流体として相互関係する粒子群それぞれの運動でモデル記述したとき、粘性流体に乱流が発生するような環境条件にて粒子群の運動がさまざまな発生器・抵抗器内外を通過して外に結合した結果として、外に伝播開始する運動エネルギー流の束のおこす音波現象がヒス音のバラエティといえる
この環境条件と現象発生程度は、粒子群の平均流速や粘度、群圧力、筒形状（含表面あらさ・筒弾性）でおよそ記述され、流体力学としてある単純計算式（レイノルズ式）で一次近似的には了解でき、また詳細には流体経験式によりおよそシミュレーションできる
粘性の量をあらわす粘度は、2枚の対向板に液をはさみ定速でずらしたときの抵抗力[N]を他パラメータで計算処理したものと定義されている（ねばる=ずらしにくい）

2.1、エアリード（楽器ならフルート・リコーダーの音源発生器近傍）の生産するヒス音
【ある温度・気圧下で振動・衝突などしている小さなランダム音波としての粘性粒子群が、別の圧力作用とストップ（障害物）に出会って加速・反射・回折し大きな音の波動現象になった場合として乱流をとらえ、声道でつくられる乱流からのヒス音のバラエティが言語信号としてたくみに利用されていることを明瞭に了解する】

2.2、フーの無声音が発生する原理と認知弁別のてがかり
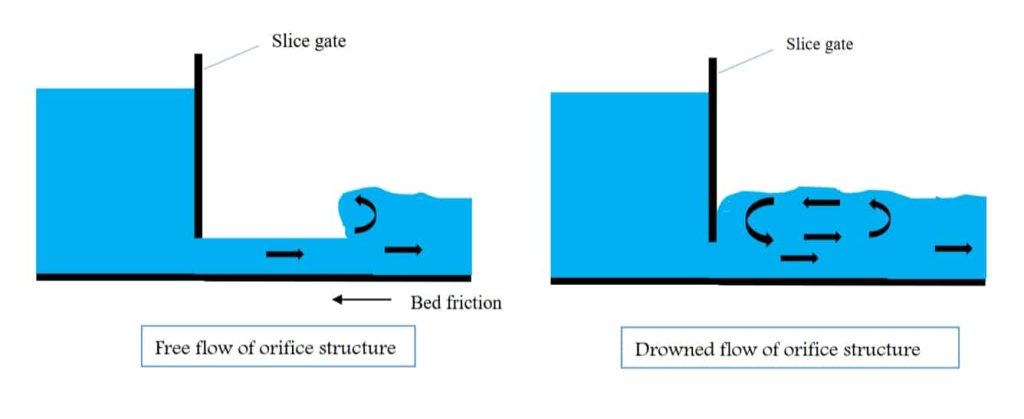
粘性のある粒子で満たされた空間に穴があいた開口/APERTURE STOPをもつ内外をわける板を立て、ある粒子流量（[個/S]など）を開口前後に通過させるには、内側の圧力を変調する方法がある このとき外に結合して伝播開始する音はヒス音である 【科学典拠・現象モデルのかみくだいた説明要、*2-3】
ここでは開口である弾性円唇筒からでる無声音の音価/PHONEを念頭に、高音のめだたない（ホワイトノイズに対しなめらかな低域通過特性をもち最低域が強調された）吹き消し音のようなヒス音として分類種類空間「フー」とラベルをつけた 以後カナを読む典型音と実際の声道音との認知対応未定義さの程度に注意

2.3、スーの無声音が発生する原理と認知弁別のてがかり
フ―と同じ原理で生産されるが、開口面積が小さく開口前後の筒諸元（厚み・弾性・断面形状）が大きく異なり流量もかせげている原因で、乱れの程度とスペクトラム包絡線がちがう（EG. 開口通過パワー密度が大きく3kHzまわりの帯域/BAND強調特性をもつなど）ことをてがかりに、これが発声音なら、歯・歯茎近傍の狭域をつかう音源発生器とその下流異形筒（～笛筒）の組から生産されるヒス音に決まっていると敏感に認知弁別できる これらをタイヤの空気漏れ音などの慣用代表的なヒス音として「スー」種とそのバラエティにとんだ亜種（「シー」「シュ―」音など）に分類するとの認知対応である

2.4、ヒーの無声音が発生する原理と認知弁別のてがかり
対向じょうご様式/CONVERGENT-DIVERGENT STYLE（EG. ゴムホース長手中間を指でつまんだ筒形状）エアリードが硬口蓋位置にありその下流の唇端との間に定在波がおこりそうなソプラノ笛筒をそなえた気道をとおって外部結合する種類のヒス音とみなすことができ有気音の典型である
以降の認知てがかりは3音とも音色からの笛種（音源発生器とその下流異形筒の組からなる）の同定が主になるだろう【内的分類指標を形成する心理機序の典拠または音価分類因の認知明瞭性の説明が必要】

2.5、グゥの維持部無声音が発生する原理と認知弁別のてがかり
対向じょうご様式エアリードが軟口蓋位置にありその下流の唇端との間に定在波をおこすのがむずかしいアルト笛筒をそなえた気道をとおって外部結合する種類のヒス音とみなすことができ各国語に特徴的な音価をつくる（EG. ピンインH[x]）

2.6、ハーの無声音が発生する原理と認知弁別のてがかり
スリット様式エアリードが声門前後の狭筒域にありその下流の声道による効率のわるいテナー笛筒全域を通って外部結合する（フー音で紙円筒入口の壁をすこし離して鳴らすのに似た）種類のヒス音とみなすことができ呼気の音の典型である

3、フーリエ変換による関数軸交代について初学者が大きく誤解しがちなこと
3.1【ある時間区間内で時間推移する線形現象の時間関数信号とその区間全体信号をフーリエ変換した周波数関数信号との可逆等価性*4 たとえば周波数関数信号はスペクトラムにあらわれる周波数情報だけでなく位相/PHASE（≜時間軸上の相互位置/MUTUAL LOCATION）情報を保っているため可逆等価信号であることの了解】

3.2【時間区間全体信号のフーリエ変換複素振幅情報からある周波数帯の時間区間全体の累積エネルギー密度[J/Hz]に比例した代表1実数だけを暫定的に中心周波数にあわせて周波数軸に並べただけの了解用省略記述法を瞬間の音色平面画像として視覚認知すること（周波数帯毎の時間区間累積エネルギー密度の平面静止図であるスペクトラムが、信号の特定瞬間の特性をどの程度正しく表現しうるかの了解 たとえば位相情報は欠落する）およびそれが時間的にコマ送りで切り替わっていく時系列推移を認知することと現実の過渡現象を必要なだけ正しく再生し了解することとの対応】

3.3、解像帯域幅および時間区間設定がつくるスペクトラム図の数学的な了解誤謬（数学的に正しいがそれを解釈する主体が直観的に間違えて認知了解するもの）
3.3.1、視覚上のスペクトラム包絡線が常に持つ周波数解像度に関連した了解誤謬
【スペクトラム図とは無限時間の中に時間区間内だけ信号がある現象全体を対象にしていて、さらには有限解像度で周波数軸信号に変換しているから、区間内部分の時間信号再生を了解するときに有限さの程度に関する誤謬が生じる】

3.3.2、スペクトラム図への偽周波数信号（エリアス）の数学的出現と時間関数にはエリアス周波数信号が区間内には含まれていない（区間内外関係がエリアスの本質的原因）ことの了解誤謬
【エリアスの含まれないスペクトラムは区間有限信号に対して存在しないのでエリアスを了解に必要なだけ小さくするために時間区間に窓関数を乗算し振幅変調することでスペクトラム介入されている（スペクトラムには常に時間区間内外関係が含まれているから原信号の再生了解時に弁別する必要がある）】

参照
1キャットフォード『実践音声学入門』（2ED、大修館2001）
2Kadam, AR. et al.. Acoustic Study and Behavior of Flow through orifices. ICDME2018. PDF700KB: https://pdf.sciencedirectassets.com/306234/1-s2.0-S2351978918X00031/1-s2.0-S2351978918300556/main.pdf
3Dowse “jbdowse.com › IPA Charts with Audio” (Accessed 2023-03-02: https://jbdowse.com/ipa/)
4Brigham, E. The Fast Fourier Transform and Its Applications. Pearson.1984. PDF8.5MB: http://sar.kangwon.ac.kr/gisg/FFT_book.pdf（宮川他訳『高速フーリエ変換』科学技術出版社）

（変更 2024-11-11）

///